Energy gap in solids

Note that as the electron becomes more localized (ie L decreases), the energy of a particular electron state (and more importantly the spacing between energy states) increases; this has important implications for bonding and also for reduced-dimensionality or quantum-confined systems .........


Kelsall, Nanoscale, Wiley, p 13


Electron as a propagating wave was first suggested by de Broglie. A wave propagating in a crystal can be disturbed by Bragg reflection. The probability to find an electron at a certain location can be calculated using the Schrodinger equation.


The first reflection and the first energy gap occurs at n=1.




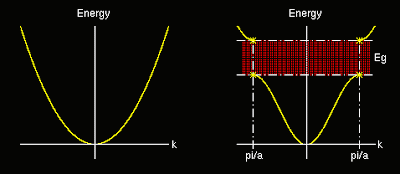
Schematic version of the parabolic relationship between the allowed electron wave vectors and their energy for electrons confined to a one dimensional potential well. The area inside the inversed curve as energy regions represent those occupied with electrons.




Changes to the system total energy


Reduction of system size may change the chemical reactivity, which will be a function of the structure and occupation of the outermost electronic energy levels. Correspondingly, physical properties such as electrical, thermal, optical and magnetic characteristics, which also depend on the arrangement of the outermost electronic energy levels, may be changed. For example, metallic systems can undergo metal -insulator transitions as the system size decreases, resulting from the formation of a forbidden energy band gap. Other properties such as mechanical strength which, to a first approximation, depends on the change in electronic structure as a function of applied stress and hence interatomic spacing, may also be affected. Transport properties may also change in that they may now exhibit a quantized rather than continuous behaviour, owing to the changing nature and separation of the electron energy levels.

Kelsall, Nanoscale Science, p 20